Next: 11.3 Discussion and Exercises Up: 11. Sorting Algorithms Previous: 11.1 Comparison-Based Sorting Contents Index
In this section we study two sorting algorithms that are not
comparison-based. Specialized for sorting small integers, these algorithms
elude the lower-bounds of Theorem 11.5
by using (parts of) the elements in
as indices into an array.
Consider a statement of the form
![$\displaystyle \ensuremath{\ensuremath{\ensuremath{\mathit{c}}[\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}]} = 1 \enspace .
$](img4371.png){kind=small}
possible
different outcomes, depending on the value of
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}$](img4373.png){kind=small}
. This means that the
execution of an algorithm that makes such a statement cannot be modelled
as a binary tree. Ultimately, this is the reason that the algorithms
in this section are able to sort faster than comparison-based algorithms.
Suppose we have an input array
consisting of
integers, each in
the range
. The counting-sort
algorithm sorts
using an auxiliary array
of counters. It outputs a sorted version
of
as an auxiliary array
.
The idea behind counting-sort is simple: For each
, count the number of occurrences of
in
and store this in
![$ \ensuremath{\ensuremath{\mathit{c}}[\ensuremath{\mathit{i}}]}$](img4384.png){kind=small}
. Now, after sorting, the output will look like
![$ \ensuremath{\ensuremath{\mathit{c}}[0]}$](img4385.png){kind=small}
occurrences of 0, followed by
![$ \ensuremath{\ensuremath{\mathit{c}}[1]}$](img4386.png){kind=small}
occurrences of 1, followed by
![$ \ensuremath{\ensuremath{\mathit{c}}[2]}$](img4387.png){kind=small}
occurrences of 2,..., followed by
![$ \ensuremath{\ensuremath{\mathit{c}}[\ensuremath{\mathit{k}}-1]}$](img4388.png){kind=small}
occurrences of
.
The code that does this is very slick, and its execution is illustrated in
Figure 11.7:
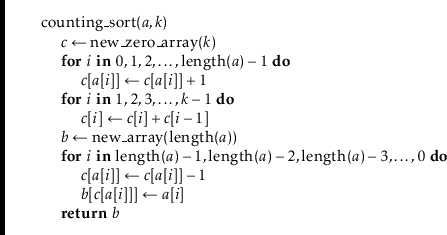
The first
loop in this code sets each counter
![$ \ensuremath{\ensuremath{\mathit{c}}[\ensuremath{\mathit{i}}]}$](img4397.png){kind=small}
so that it
counts the number of occurrences of
in
. By using the values
of
as indices, these counters can all be computed in
time
with a single for loop. At this point, we could use
to
fill in the output array
directly. However, this would not work if
the elements of
have associated data. Therefore we spend a little
extra effort to copy the elements of
into
.
The next
loop, which takes
time, computes a running-sum
of the counters so that
![$ \ensuremath{\ensuremath{\mathit{c}}[\ensuremath{\mathit{i}}]}$](img4409.png){kind=small}
becomes the number of elements in
that are less than or equal to
. In particular, for every
, the output array,
, will have
![$\displaystyle \ensuremath{\ensuremath{\ensuremath{\mathit{b}}[\ensuremath{\math...
...\mathit{i}}]-1}]}=\ensuremath{\ensuremath{\ensuremath{\mathit{i}}}} \enspace .
$](img4414.png){kind=small}
backwards to place its elements, in order,
into an output array
. When scanning, the element
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{i}]\gets \ensuremath{j}}$](img4417.png){kind=small}
is placed
at location
![$ \ensuremath{\ensuremath{\mathit{b}}[\ensuremath{\mathit{c}}[\ensuremath{\mathit{j}}]-1}]$](img4418.png){kind=small}
and the value
![$ \ensuremath{\ensuremath{\mathit{c}}[\ensuremath{\mathit{j}}]}$](img4419.png){kind=small}
is decremented.
method can sort an array
containing
integers in the set
in
time.
The counting-sort algorithm has the nice property of being stable;
it preserves the relative order of equal elements. If two elements
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}$](img4425.png){kind=small}
and
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{j}}]}$](img4426.png){kind=small}
have the same value, and
then
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}$](img4428.png){kind=small}
will
appear before
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{j}}]}$](img4429.png){kind=small}
in
. This will be useful in the next section.
Counting-sort is very efficient for sorting an array of integers when the
length,
, of the array is not much smaller than the maximum value,
, that appears in the array. The radix-sort
algorithm,
which we now describe, uses several passes of counting-sort to allow
for a much greater range of maximum values.
Radix-sort sorts
-bit integers by using
passes of counting-sort
to sort these integers
bits at a time.11.2 More precisely, radix sort first sorts the integers by
their least significant
bits, then their next significant
bits,
and so on until, in the last pass, the integers are sorted by their most
significant
bits.
(In this code, the expression
![$ \ensuremath{(\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]\ensuremath{\gg}\...
...remath{\mathit{d}}\cdot \ensuremath{\mathit{p}})} \wedge (\ensuremath{2^{d}-1})$](img4444.png){kind=small}
extracts the integer
whose binary representation is given by bits
of
![$ \ensuremath{\ensuremath{\mathit{a}}[\ensuremath{\mathit{i}}]}$](img4446.png){kind=small}
.)
An example of the steps of this algorithm is shown in Figure 11.8.
![\includegraphics[width=\textwidth ]{figs-python/radixsort}](img4447.png)
|
This remarkable algorithm sorts correctly because counting-sort is
a stable sorting algorithm. If
are two elements of
,
and the most significant bit at which
differs from
has index 
,
then
will be placed before
during pass
and subsequent passes will not change the relative order of
and
.
Radix-sort performs
passes of counting-sort. Each pass requires
time. Therefore, the performance of radix-sort is given
by the following theorem.
If we think, instead, of the elements of the array being in the range
, and take
we obtain
the following version of Theorem 11.8.
divides
, otherwise we can always increase
to
.
![\includegraphics[width=\textwidth ]{figs-python/countingsort}](img4391.png)
